Presentation
Here is a 🏎️ quick presentation, in simple words, of what coq-of-solidity does.
With
coq-of-solidityyou make sure that the money stored on your Solidity smart contract cannot be stolen. 🛡️
Every month, millions of dollars 💰 are stolen from smart contracts. This is because a single mistake in the code, even if this is just one line, lets an attacker withdraw all the money and disappear with it!
Audits are mandatory, but this is a human 🧠 verifying the code, and mistakes are made.
🚨 Even if major smart contracts have all been audited, they are still regularly hacked.
With coq-of-solidity, the computer checks that the reasoning of the auditor is correct: this is like a spell checker for auditors.
As a result, you can truly be sure that no attack scenario has been forgotten and that your smart contract is truly secure ✅.
In addition, when you update the code of your smart contract, you can replay the reasoning for free to make sure your smart contract is still secure on the old part 😎 . This saves on auditing costs.
Why us?
Verifying reasoning about code is called 🔎 formal verification. This is a complex technique 🧪 and very few companies have developed a tool to do this for Solidity. In addition, coq-of-solidity is the only one with Clear that can express any possible reasoning/property on your code. This is thanks to the use of an 🐓 interactive theorem prover on the backend.
At 🌲 Formal Land, where we developed coq-of-solidity, we are one of the leading teams applying formal verification to large-scale programs. We have developed two other formal verification tools, with coq-of-rust for 🦀 Rust and coq-of-ocaml for 🐫 OCaml. Read more about what we do on our 📖 blog.
How much? 💸
For a large smart contract (5,000 lines of Solidity), consider a price of $50,000 for a formal verification of a model of the code, and $100,000 for a verification at the level of the source code (more precise). So, this is competitive with traditional audits in terms of pricing.
💌 Contact us for an evaluation!
coq-of-solidityis fully open-source, under MIT licence, so you can also use it by yourself! 🚀
Introduction
coq-of-solidity is a tool to formally verify properties about smart contracts written in 🪨 Solidity. Formal verification is about checking properties on a program for every possible input. This contrasts with testing, which only checks a finite number of cases. It is the most powerful way to ensure your code is bug-free! ✅ It was originally developed for critical software in 🧑🚀 space systems, nuclear plants, etc. but it is now becoming more and more popular for the blockchain.
In the rest of the documentation, we assume you have some knowledge in formal verification and in particular in the 🐓 Coq proof assistant which we use. On a general note, expect it to be harder to fully formally verify a program than to write it. Still, it must be the simplest way to truly ensure your program is correct.
What you get
Thanks to coq-of-solidity, you can:
- Prove that your smart contract is safe 🛡️ for any possible inputs or successions of calls.
- Prove that your business rules are always respected.
- Run these checks in your CI/CD pipeline to ensure that no bug is introduced in your codebase.
This adds a final layer of security to traditional code audits which are based on human reasoning and testing which only checks a finite amount of cases. This verification even goes beyond other formal verification methods.
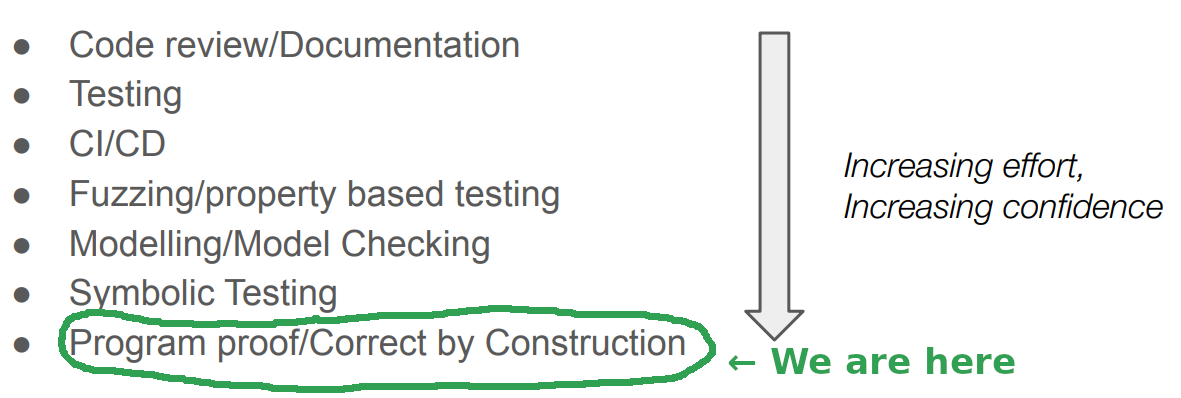 Picture from a presentation of Galois
Picture from a presentation of Galois
Typical workflow
Formal verification is expensive ⏲️, so you should apply it after every other verification (testing, code review, etc.) is done. Here is a typical workflow:
- You model your smart contract in the Coq proof system. For this step, you manually rewrite your smart contract in idiomatic Coq code.
- You start expressing and proving a few properties in Coq about your model. For example, for any possible call the total number of tokens in your contract is constant, if that is a business rule.
- Once you are confident in the approach, you show that your model is equivalent to the Solidity source code using
coq-of-solidityand integrate this check into your CI/CD pipeline. At this step, you will probably discover some differences between your model and the source code, like unaccounted integer overflows, and you will have to refine your model to take them into account. - When your code evolves, you can update your model and your proofs to ensure that your new code is still correct.
coq-of-soliditywill make sure that your model is still equivalent to your source code 🚀.
Example
Here is an example of Solidity function returning the standard addition ➕:
function add(uint256 a, uint256 b) public pure returns (uint256) {
return a + b;
}
Here is its translation to Coq as generated by coq-of-solidity:
Definition checked_add_t_uint256 (x : U256.t) (y : U256.t) : M.t U256.t :=
let~ '(_, (sum, x, y)) :=
let sum := 0 in
let~ x := [[ cleanup_t_uint256 ~(| x |) ]] in
let~ y := [[ cleanup_t_uint256 ~(| y |) ]] in
let~ sum := [[ add ~(| x, y |) ]] in
let_state~ 'tt := [[
Shallow.if_ (|
gt ~(| x, sum |),
do~ [[ panic_error_0x11 ~(||) ]] in
M.pure (BlockUnit.Tt, tt),
tt
|)
]] default~ (sum, x, y) in
M.pure (BlockUnit.Tt, (sum, x, y))
in
M.pure sum.
This translation is a bit more low-level as we rely on the intermediate language Yul of the Solidity compiler. Here is what it does in pseudo-code:
function checked_add_t_uint256(x, y) {
sum := x + y modulo 2^256
if x > sum {
panic
}
return sum
}
For security, the addition in Solidity checks the overflows and panics if it happens. Here is the Coq model of the addition:
Definition safe_add (x y : Z) : option Z :=
(* We use unbounded integers [Z] *)
let sum := x + y in
(* We return [None] in case of overflow *)
if sum <? 2 ^ 256 then
Some sum
else
None.
We can express that it behaves as the translation of the Solidity code in the non-overflown case:
Lemma run_checked_add_t_uint256 codes environment state
(x y sum : Z)
(H_x : 0 <= x < 2^256)
(H_y : 0 <= y < 2^256)
(H_sum : safe_add x y = Some sum) :
{{? codes, environment, Some state |
checked_add_t_uint256 x y ⇓
Result.Ok sum
| Some state ?}}.
It says that for any initial chain state and x and y such that they are in the range of uint256, if the addition does not overflow, then the result of the translation is the sum of x and y, and the chain state is unchanged. We could make a similar statement for the overflow case.
Now, we need to prove that this statement is true using the tactic language of Coq and some of the custom tactics provided by coq-of-solidity. We write the proof using the interactive mode of Coq. To give an idea, here is our proof:
Proof.
unfold safe_add in H_sum.
destruct (_ <? _) eqn:? in H_sum; inversion_clear H_sum.
unfold checked_add_t_uint256.
lu.
repeat (lu || cu || p).
s.
unfold Pure.gt, Pure.add.
destruct (_ >? _) eqn:?; s.
{ lia. }
{ pe; f_equal.
lia.
}
Qed.
How it works
We make a shallow embedding of Yul into Coq. All the code is put into a monad to represent the various side-effects which are mainly:
- Modifying the blockchain state.
- Control-flow operations, such as
breakorcontinuein a loop, orrevertto prematurely abort a contract. - Mutating the local variables.
We translate the mutation of variables by doing an effect analysis and building a state that is the tuple of the variables being currently updated. This helps to reason about loops.
We recommend only translating the unoptimized version of Yul. That way you are sure to:
- Keep the same variable names in the Coq translation as in the source Solidity, helping for the proof process.
- Have a diff in the translation that is proportional to the diff in the source code.
The implementation of coq-of-solidity is actually fairly simple and relies on the existing Coq system for the heavy work! 🏋️
Getting Started
Here we give you the instructions to get started to translate Solidity smart contracts to Coq.
Translate Solidity to Coq
If you have a smart contract named contract.sol, generate the JSON of its unoptimized Yul code with the following command:
solc --ir-ast-json contract.sol \
| tail -1 \
> contract.yul.json
assuming you have installed the Solidity compiler solc.
Then clone the repository of coq-of-solidity:
git clone https://github.com/formal-land/coq-of-solidity.git
cd coq-of-solidity
Then translate it to Coq with the following command:
python coq/scripts/shallow_embed.py path/to/contract.yul.json \
> shallow.v
The resulting file shallow.v contains the Coq code of the smart contract. Generally the first part is the deployment code (constructor), and then comes the code for the entrypoints of the smart contract.
Compile the generated Coq code
Assuming you have a working installation of the opam package manager that we use for Coq, from the root of the coq-of-solidity repository, run the following command to install the CoqOfSolidity library:
opam install --deps-only coq/CoqOfSolidity/coq-of-solidity.opam
Then go to the directory with the Coq code:
cd coq/CoqOfSolidity
Compile and install the CoqOfSolidity library:
make -j3
make install
You can now compile your generated shallow.v file, for example opening it in VSCode with the Coq extension installed.